6ºs Matemática

SETEMBRO

ÁREAS

AGOSTO

Potências

Potências com nº naturais

Jogo da potência

Jogo da velha - Potência

Potenciação: Definição e Exemplos

0 Comentário

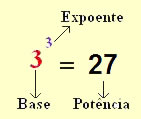
Potência

PUBLICIDADE

Podemos dizer que potenciação representa uma multiplicação de fatores iguais, se temos a seguinte multiplicação: 2 x 2 x 2 x 2 x 2 x 2, podemos representá-la usando a potência 2⁶, onde 2 é a base e 6 o expoente (Leia: dois elevado a sexta potência).

O expoente possui um papel fundamental na potenciação, pois ele é quem define quantas vezes a base será multiplicada por ela mesma. Observe:

2⁶ = 2 x 2 x 2 x 2 x 2 x 2 = 64
4² = 4 x 4 = 16
5³ = 5 x 5 x 5 = 125
10² = 10 x 10 = 100
12² = 12 x 12 = 144
3⁵ = 3 x 3 x 3 x 3 x 3 = 243
6³ = 6 x 6 x 6 = 216

Casos de potenciação

Todo número diferente de zero e elevado a zero é um.
2⁰ = 1
3⁰ = 1
10⁰ = 1
4⁰ = 1
125⁰ = 1

Todo número diferente de zero e elevado a um é o próprio número.
2¹ = 2
3¹ = 3
15¹ = 15
20¹ = 20
12¹ = 12

Base zero e qualquer número no expoente, o resultado será zero.
0⁵ = 0
0¹² = 0
0¹⁰⁰ = 0
0⁷ = 0
0²⁵ = 0

Base negativa e expoente ímpar, resultado negativo.
(-3)³ = (-3) x (-3) x (-3) = -27
(-4)⁵ = (-4) x (-4) x (-4) x (-4) x (-4) = -1024
(-2)⁷ = (-2) x (-2) x (-2) x (-2) x (-2) x (-2) x (-2) = -128

Base negativa e expoente par, resultado positivo.
(-2)⁴ = (-2) x (-2) x (-2) x (-2) = + 16
(-6)² = (-6) x (-6) = + 36
(-7)² = (-7) x (-7) = + 49

Base é um número racional (fração): devemos elevar ao expoente indicado o numerador e o denominador da fração.



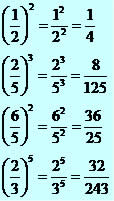
Quando o expoente é um número negativo: invertemos a base e mudamos o sinal do expoente para positivo.




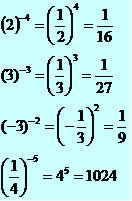
Uma importante aplicação de potenciação é a notação científica, usada para expressar valores muito grandes ou muito pequenos. A notação é usada por cientistas, como astrônomos, físicos, biólogos, químicos entre outros.

Exemplos: 
6 120 000, podemos representá-lo usando a seguinte notação decimal 6,12 * 10⁶

0,00012, pode ser representado por 1,2 * 10^-4.

JUNHO


Aritmética RC
Calculadora Quebrada
Calculando

Expressão numerica - RC

...................................................................................................

MAIO

Tabuada - Arraste e solte
Multiplicação - Stun attack
Multiplicação Memória

........................................................................................................................................

ABRIL 



Sequência Numérica

http://jogosonlinegratis.uol.com.br/jogoonline/sum-tracks/

Caça Resultados




MARÇO

Jogo das Contas (+ - x :)


Somar - Horas e minutos

FEVEREIRO

Revisão:
Soma e Subtração
Situação Problema
Algarismos Romanos








............................................................................

CONTEÚDOS

Carta Enigmática


Toytheater - Matemática

Bingo


Caça palavras - Matemática



QUIZ - Matemática

Memória - Multiplicação

Problemas - Dinheiro

Atividades Matemática - Porto Alegre - Ludica


**************************************************************

FRAÇÕES

Frações II - Escolovar
Frações III - Escolovar
Pizza - Escola Games

Fração é considerada parte de um inteiro, que foi dividido em partes exatamente iguais. As frações são escritas na forma de números e na forma de desenhos. Observe alguns exemplos:

O inteiro foi divido em 6 partes, onde 1 delas foi pintada.

O inteiro foi dividido em 9 partes, onde 6 foram pintadas.

O inteiro foi dividido em 4 partes, onde 1 fora pintada.


Na fração, a parte de cima é chamada de numerador, e indica quantas partes do inteiro foram utilizadas.
A parte de baixo é chamada de denominador, e indica a quantidade máxima de partes em que fora dividido o inteiro.

Observe a leitura e a representação das seguintes frações.

Um meio

Um terço

Um quarto

Um quinto

Dois sextos



Dois nonos

Cinco sétimos

Três décimos

Quatro oitavos


Quando o denominador da fração é 10, 100 ou 1000, a fração deve ser escrita utilizando décimos, centésimos e milésimos. Observe:

Quatro décimos

Quatro centésimos

Quatro milésimos


Nas situações em que o denominador é maior que 10, escrevemos a palavra avos junto ao nome da fração.


Dois treze avos


Cinco dezenove avos

Doze vinte avos

...............................................................................................................

POLÍGONOS E POLIEDROS


Colorir Poliedros
Poliedros 6 faces



...............................................................................................................

MMC e MDC - Roleta


MÍNIMO MÚLTIPLO COMUM (M.M.C)

O mínimo múltiplo comum entre dois números naturais é obtido a partir da interseção dos múltiplos naturais, escolhendo-se o menor excetuando o zero. O m.m.c pode ser calculado pelo produto de todos os fatores primos, considerados uma única vez e de maior expoente.

Exemplo: 120 e 36

120  2                 36   2
60    2                 18   2
30    2                  9    3
15    3                  3    3
5      5                  1    2².3²
1      2³.3.5

m.m.c ( 120, 36) = 2³.3².5 = 360

O m.m.c também pode ser calculado pela decomposição simultânea em fatores primos.

120   –   36   2
60     –   18   2
30     –   9     2
15     –   9     3
5       –   3     3
5       –   1     5
1       –   1     2³.3².5 = 360

MÁXIMO DIVISOR COMUM (M.D.C)

O máximo divisor comum (mdc) entre dois números naturais é obtido a partir da interseção dos divisores naturais, escolhendo-se o maior.

O mdc pode ser calculado pelo produto dos fatores primos que são comuns tomando-se sempre o de menor expoente.

Exemplo: 120 e 36

120   2                  36    2
60     2                  18    2
30     2                   9     3
15     3                   3     3
5       5                  1      2².3²
1       2³.3.5

m.d.c ( 120, 36) = 2².3 = 12

O m.d.c também pode ser calculado pela decomposição simultânea em fatores primos, tomando apenas os fatores que dividem simultaneamente.

120 –   36   2 ( * )
60   –   18   2 ( * )
30   –   9     2
15   –   9     3 ( * )
5     –   3     3
5     –   1     5
1     –   1     2².3 = 12

...........................................................................................................................


Multiplique

Teste com expressões numéricas